The shoelace formula can computes the area of a quadrilateral from the points coordinates . The formula requires that the points are taken clockwise or counter clockwise, that is a quadrilateral must not be self crossing.
A criterion implemented in python was proposed to check if two segments are intersecting, which should be the case for a self-crossing quadrilateral.
A criterion implemented in python was proposed to check if two segments are intersecting, which should be the case for a self-crossing quadrilateral.
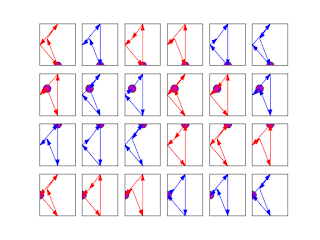
With four points, there is 4!=24 ways to calculate the area. With points defining a square, according to the points order, the area takes three values: -2, 0 and 2 for indirect, self crossing and direct square:
The first square (top left in red) defined by the points (1, 0), (2, 1), (1, 2), (0, 1):
 |
| The first point is the purple one. |
((1, 0), (2, 1), (1, 2), (0, 1)) False 2.0
is detected as non self crossing (False), and the shoelace formula gives an area equal to 2 as waited for this direct square. There is a problem for some self crossing quadrilaterals:
((1, 0), (2, 1), (0, 1), (1, 2)) False 0.0
((1, 0), (1, 2), (2, 1), (0, 1)) True 0.0
((1, 0), (1, 2), (2, 1), (0, 1)) True 0.0
The second quadrilateral is not detected as self crossing, however the shoelace formula yield an area equal to zero, as the third quadrilateral which is correctly dtected as self crossing (True). The last quadrilateral (blue one, down right):
((0, 1), (1, 2), (2, 1), (1, 0)) False -2.0
is correctly deteted as non self crossing (False) and indirect with a negative "area" equal to -2
Trying with points yielding non convex quadrilaterals yields six values -0.95,-0.65, -0.4, 0.4, 0.65, 0.95. None is detected as self crossing:
With other points defining a possible convex quadrilateral:
Several values are found. The maximal area value : 1.465, corresponds to the four simple quadrilaterals (non self crossing):
((1.1, 0.3), (1.7, 1.4), (1, 2), (0, 1)) False 1.465
((1.7, 1.4), (1, 2), (0, 1), (1.1, 0.3)) False 1.465
((1, 2), (0, 1), (1.1, 0.3), (1.7, 1.4)) False 1.465
((0, 1), (1.1, 0.3), (1.7, 1.4), (1, 2)) False 1.465
It seems that the maximal area value found from the set of 24 possible quadrilaterals correspond to simple direct quadrilaterals, thus testing if the four points define a non self crossing quadrilateral may not be usefull.
January 3, 2013:
The script is modified so that the quadrilaterals are plotted with matplotlib.patches.Polygon:
Download code
Play with the code on cloud.sagemath.com